Minkowski dimension calculator (QGIS plugin)

Fractal dimension and GIS data

Many real-world geographies look “messy” at first glance - coastlines, river networks, city edges, even patchy habitats. That messiness isn’t random, it is often scale-dependent and well described by fractal geometry. The classic coastline paradox showed that measured length grows as your measuring stick shrinks, a pattern captured by a number called the fractal dimension, which quantifies how “space-filling” a shape is.

This article introduces a QGIS module that estimates the Minkowski–Bouligand (box-counting) fractal dimension for vector features. It works directly on linear boundaries and is practical for everyday geospatial analysis. Attach fractal dimension as an attribute, style by value, filter by thresholds, and compare features across regions or time.

How does Minkowski dimension work

Technically, its calculation can be reduced to the following procedure:

• The object is covered with a square grid of cells of known size.
• The number of cells containing a fragment of the studied object is counted. A pair of values is recorded: “cell size (side length)” – “number of cells containing the object”.
• The grid is refined, i.e., the cell size is decreased, and accordingly, the number of cells containing the object increases. A new pair of values is recorded.
• The refinement procedure is repeated multiple times.

As an example, let us count the number of squares and their sizes for a given polygon. We obtain the following two series:

Cell sizes (e):
[200000, 195365, 190731, 186097, 181463, 176829, 172195, 167560, 162926, 158292, 153658, 149024, 144390, 139756, 135121, 130487, 125853, 121219, 116585, 111951, 107317, 102682, 98048, 93414, 88780, 84146, 79512, 74878, 70243, 65609, 60975, 56341, 51707, 47073, 42439, 37804, 33170, 28536, 23902, 19268, 14634, 10000]

Number of cells containing the object (N):
[44, 44, 43, 41, 44, 46, 49, 48, 52, 52, 54, 58, 59, 62, 62, 67, 64, 74, 77, 76, 87, 88, 96, 90, 106, 111, 120, 122, 143, 149, 158, 181, 192, 217, 242, 276, 333, 380, 458, 584, 799, 1223]

According to the method for calculating the Minkowski dimension, its value equals the slope of the regression line constructed on the plane using the series of values log(N) and log(1/e). For clarity, let us illustrate this with a graph and a regression line.

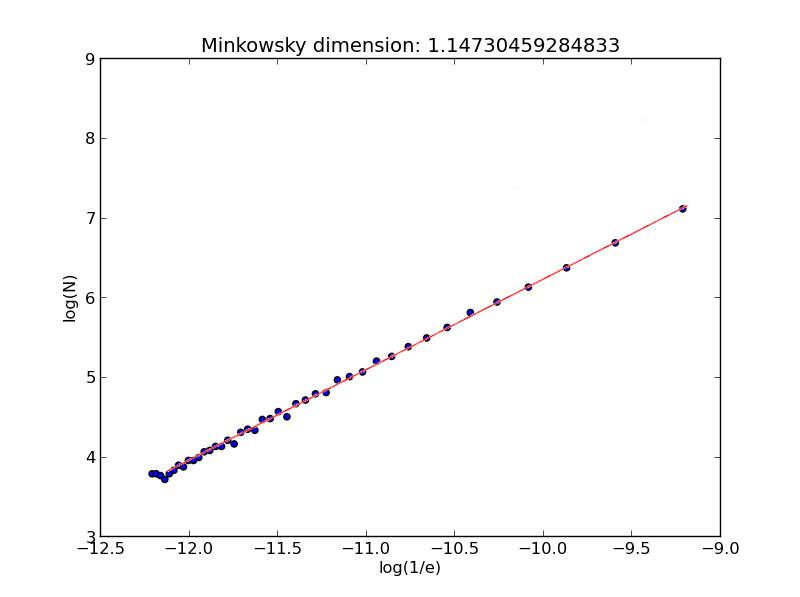
The resulting dimension is 1.145.

Such calculations are repeated independently for each object of interest.

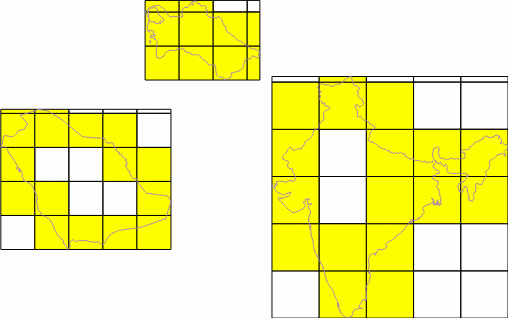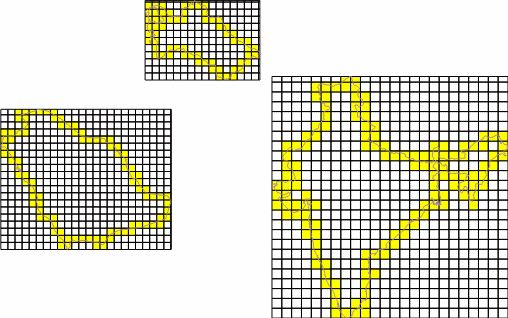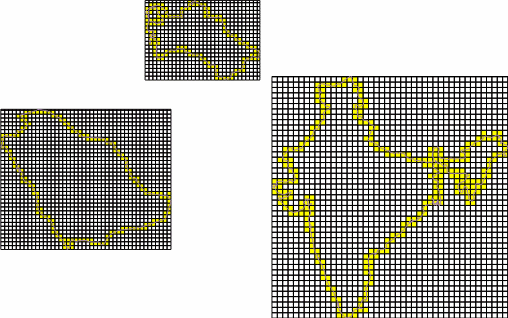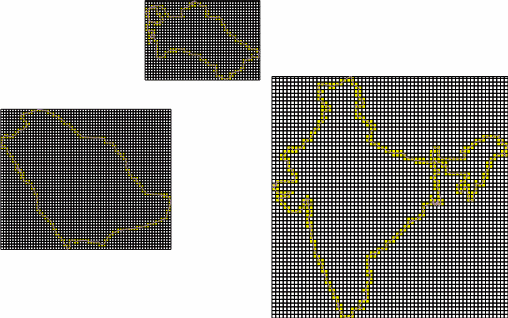
Areas of applicability

Along with the development of the theoretical foundations of fractal geometry, attempts arose to apply them in the natural sciences - geology, geography, biology, and others. Today, there are numerous articles and even extensive books [1,2] devoted to various aspects of the geographical interpretation of fractals.

In urban studies, researchers often attempt to link different aspects of urban space with the fractal dimension of city contours and its changes over time. For example, here are the fractal dimensions of major world cities [3]:

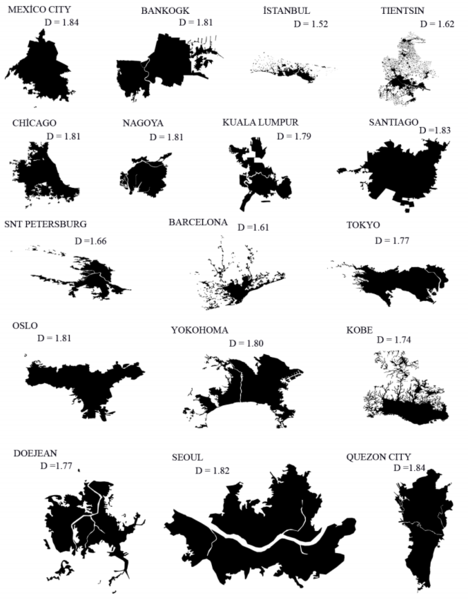
The authors assess fractal dimensions together with a large set of socio-economic indicators of urban development, such as the Human Development Index, vehicle ownership rates, population dynamics, and others.

A considerable body of research in urban studies is devoted to fractal analyses of transportation networks [4], city boundaries (including with the use of the Minkowski dimension [5]), and other aspects [6]. Fractals also attract broad interest in hydrology. Assessing the fractal characteristics of river systems makes it possible to expand the understanding of their genesis, predict further developmental dynamics, and evaluate the relationships between different geometric and hydrodynamic parameters of rivers [7, 8].

Similar studies can be found in the fields of landscape science [9], geobotany [10], physical geography [11], ecology [12], and many others.

QGIS Plugin

Minkowski Dimension Calculator is a simple plugin assessing fractal dimensions for features of a linear vector layer. It adds a tool to the Processing Toolbox. It allows you to:

• Select an input layer.
• Set up several opti0nal parameters.
• Automatically calculate Minkowski dimension values and add them as attribute values for each feature. Also confidence level is calculated to the separate field.

Tool interface and result layer colored by fractal dimension value:

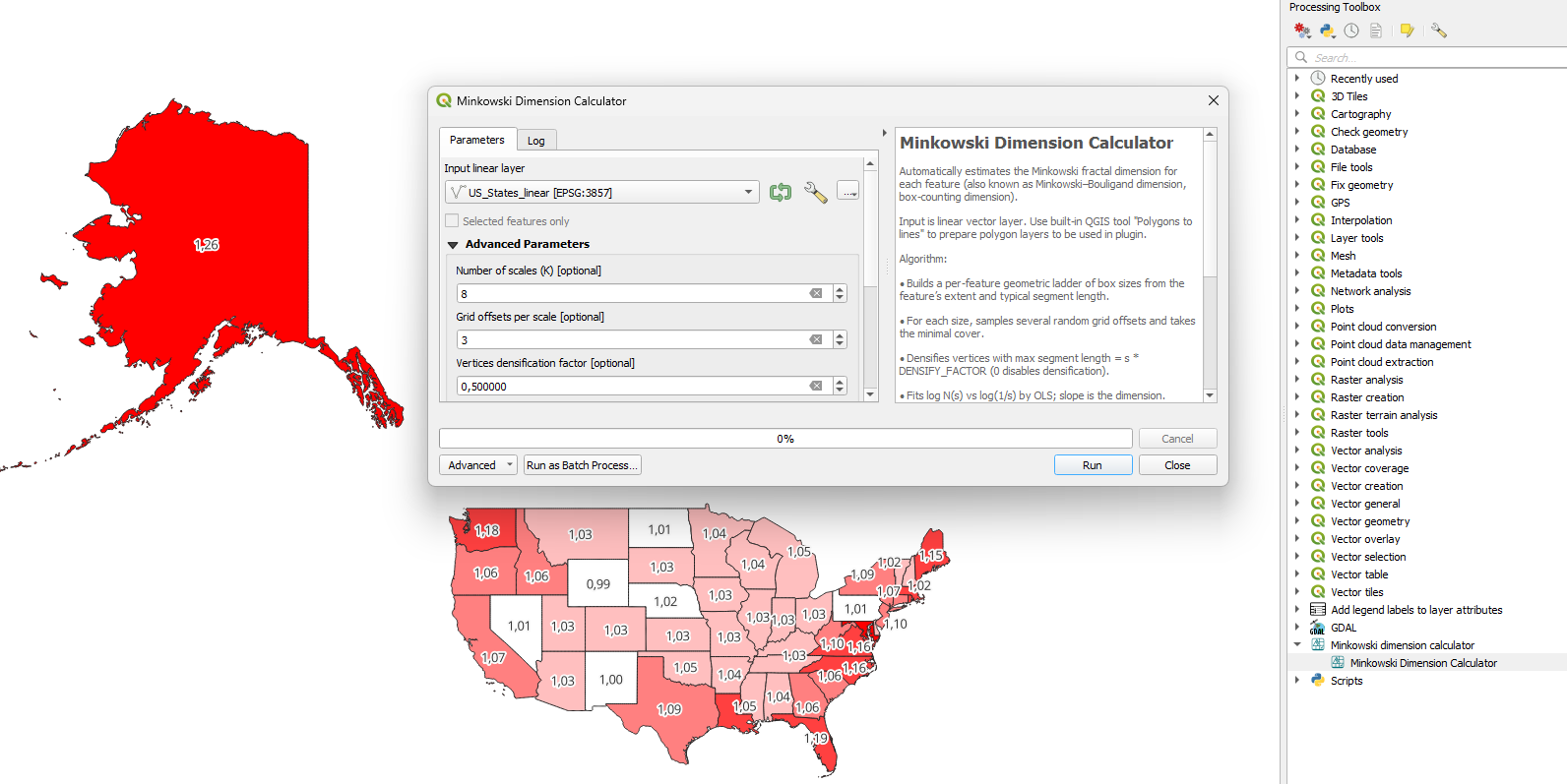
Technically, results are two new columns added to the input layer:

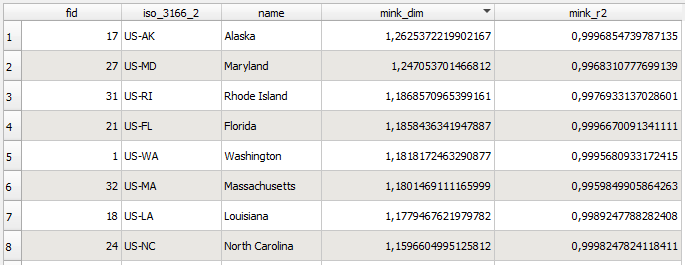
You could run the tool with default option values in most cases. Options are:

1. Number of scales (K): to put more points along the log–log line (8–12 typical).
2. Grid offsets per scale: mitigates grid alignment bias (3–5 typical).
3. Densification factor: controls vertex insertion density at each scale; 0.5 is a good default. Higher value -> more dense geometry to be analyzed.
4. Output field name for dimension value
5. Output field name for R2 value (confidence level. Values below 0.85 should be considered as very unconfident)

If you found a bug, have questions or suggestions, please contact me, I would be glad to improve the Plugin.